Last Updated on Mar 31, 2016
0 of 10 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
Quiz Description :
Name: Angular Motion objective question answer quiz
Subject: Physics
Topic: Motion
Questions: 10 Objective Type
Time Allowed: 15 Minutes
Important for: 11th & 12th School students, Engineering and Medical Entrance exams, B Sc / M Sc Entrance and University exam.
You have already completed the quiz before. Hence you can not start it again.
quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
You have Completed " Angular Motion objective question answer quiz "
0 of 10 questions answered correctly
Your time:
Time has elapsed
Your Final Score is : 0
You have attempted : 0
Number of Correct Questions : 0 and scored 0
Number of Incorrect Questions : 0 and Negative marks 0
| Average score |
|
| Your score |
|
-
Not categorized
You have attempted: 0
Number of Correct Questions: 0 and scored 0
Number of Incorrect Questions: 0 and Negative marks 0
-
It’s time to share this quiz with your friends on Facebook, Twitter, Google Plus, Whatsapp or LinkedIn…
Click on View Questions Button to check Correct and incorrect answers.
Login
Register
Forgot Password
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Answered
- Review
-
Question 1 of 10
1. Question
1 pointsA couple produces
Correct
We know that two equal and unlike parallel forces acting on a body form a couple. And moment of the couple is equal to the product of the magnitude of either force and perpendicular distance between the lines of action of the forces.
This couple tends the body to have purely rotational motion.Incorrect
We know that two equal and unlike parallel forces acting on a body form a couple. And moment of the couple is equal to the product of the magnitude of either force and perpendicular distance between the lines of action of the forces.
This couple tends the body to have purely rotational motion.Unattempted
We know that two equal and unlike parallel forces acting on a body form a couple. And moment of the couple is equal to the product of the magnitude of either force and perpendicular distance between the lines of action of the forces.
This couple tends the body to have purely rotational motion. -
Question 2 of 10
2. Question
1 pointsThe angular velocity of a wheel is 70 rad-s-1. If radius of the wheel is 0.5m, then linear velocity of the wheel is
Correct
Given: Angular velocity of wheel (ω) = 70 rad-s-1 and radius of wheel (r) = 0.5m.
We know that linear velocity of the wheel (v) = ω r = 70 × 0.5 = 35 m-s-1Incorrect
Given: Angular velocity of wheel (ω) = 70 rad-s-1 and radius of wheel (r) = 0.5m.
We know that linear velocity of the wheel (v) = ω r = 70 × 0.5 = 35 m-s-1Unattempted
Given: Angular velocity of wheel (ω) = 70 rad-s-1 and radius of wheel (r) = 0.5m.
We know that linear velocity of the wheel (v) = ω r = 70 × 0.5 = 35 m-s-1 -
Question 3 of 10
3. Question
1 pointsA dics of radius 1m is rotating with an angular velocity of 10 rad-s-1. The linear velocity of the dics on a point on a point 0.5m from its centre is
Correct
Given: Radius of dics (r) = 1m; Angular velocity of dics (ω) = 10 rad-s-1 and distance of the point from its centre (d) = 0.5m.
We know that linear velocity of dice on its extreme point (v) = d ω = 0.5 × 10 = 5 m-s-1.Incorrect
Given: Radius of dics (r) = 1m; Angular velocity of dics (ω) = 10 rad-s-1 and distance of the point from its centre (d) = 0.5m.
We know that linear velocity of dice on its extreme point (v) = d ω = 0.5 × 10 = 5 m-s-1.Unattempted
Given: Radius of dics (r) = 1m; Angular velocity of dics (ω) = 10 rad-s-1 and distance of the point from its centre (d) = 0.5m.
We know that linear velocity of dice on its extreme point (v) = d ω = 0.5 × 10 = 5 m-s-1. -
Question 4 of 10
4. Question
1 pointsA point on the rim of a wheel of diameter 400 cm has a velocity of 16 m-s-1. The angular velocity of the wheel is
Correct
Given that diameter of wheel (d) = 400cm = 4m or Radius (r) = 2m and velocity of the point on the rim (v) = 16 m-s-1.
We know that angular velocity of wheel (ω) = v/r = 16/2 = 8 rad-s-1.Incorrect
Given that diameter of wheel (d) = 400cm = 4m or Radius (r) = 2m and velocity of the point on the rim (v) = 16 m-s-1.
We know that angular velocity of wheel (ω) = v/r = 16/2 = 8 rad-s-1.Unattempted
Given that diameter of wheel (d) = 400cm = 4m or Radius (r) = 2m and velocity of the point on the rim (v) = 16 m-s-1.
We know that angular velocity of wheel (ω) = v/r = 16/2 = 8 rad-s-1. -
Question 5 of 10
5. Question
1 pointsIf a flywheel makes 120 rev-min-1, then its angular speed will be
Correct
Given that angular frequency of flywheel (N) = 120 rev-min-1 = 2 rev-s-1.
We know that angular speed of the flywheel (ω) = 2 π N = 2 π × 2 = 4 π rad-s-1.Incorrect
Given that angular frequency of flywheel (N) = 120 rev-min-1 = 2 rev-s-1.
We know that angular speed of the flywheel (ω) = 2 π N = 2 π × 2 = 4 π rad-s-1.Unattempted
Given that angular frequency of flywheel (N) = 120 rev-min-1 = 2 rev-s-1.
We know that angular speed of the flywheel (ω) = 2 π N = 2 π × 2 = 4 π rad-s-1. -
Question 6 of 10
6. Question
1 pointsAn engine flywheel of diameter 1m rotates with an angular velocity of 600 rev-min-1. The linear velocity of a particle on the periphery of the wheel will be
Correct
Given that diameter of flywheel (d) = 1m or Radius (r) = 0.5m and angular frequency of flywheel (N) = 600 rev-min-1 = 10 rev-s-1.
We know that angular speed of flywheel (ω) = 2 π N = 2 π × 10 = 20 π m-s-1.
Therefore linear velocity of a particle on the periphery of the wheel (v) = ωr
= 0.5 × 20 π = 10 π m-s-1.Incorrect
Given that diameter of flywheel (d) = 1m or Radius (r) = 0.5m and angular frequency of flywheel (N) = 600 rev-min-1 = 10 rev-s-1.
We know that angular speed of flywheel (ω) = 2 π N = 2 π × 10 = 20 π m-s-1.
Therefore linear velocity of a particle on the periphery of the wheel (v) = ωr
= 0.5 × 20 π = 10 π m-s-1.Unattempted
Given that diameter of flywheel (d) = 1m or Radius (r) = 0.5m and angular frequency of flywheel (N) = 600 rev-min-1 = 10 rev-s-1.
We know that angular speed of flywheel (ω) = 2 π N = 2 π × 10 = 20 π m-s-1.
Therefore linear velocity of a particle on the periphery of the wheel (v) = ωr
= 0.5 × 20 π = 10 π m-s-1. -
Question 7 of 10
7. Question
1 pointsA fan is making 600 rev-min-1. If it makes 1200 rev-m-1, then increase in its angular velocity is
Correct
Given that initially angular frequency (N1) = 600 rev-m-1 = 10 rev-s-1 and final angular frequency (N2) = 1200 rev-min-1 = 20 rev-s-1.
We know that increase in angular velocity (∆ω) = ω2 – ω1 = 2 π N2 – 2 π N1 = (2π × 20) – (2π × 10)
= (40 π × 20 π) = 20 π rad-s-1.Incorrect
Given that initially angular frequency (N1) = 600 rev-m-1 = 10 rev-s-1 and final angular frequency (N2) = 1200 rev-min-1 = 20 rev-s-1.
We know that increase in angular velocity (∆ω) = ω2 – ω1 = 2 π N2 – 2 π N1 = (2π × 20) – (2π × 10)
= (40 π × 20 π) = 20 π rad-s-1.Unattempted
Given that initially angular frequency (N1) = 600 rev-m-1 = 10 rev-s-1 and final angular frequency (N2) = 1200 rev-min-1 = 20 rev-s-1.
We know that increase in angular velocity (∆ω) = ω2 – ω1 = 2 π N2 – 2 π N1 = (2π × 20) – (2π × 10)
= (40 π × 20 π) = 20 π rad-s-1. -
Question 8 of 10
8. Question
1 pointsA flywheel starts form rest and gains a speed of 540 rev-min-1 in 6s. Angular acceleration of the flywheel will be
Correct
Given that initially angular frequency (N1) = 0 (because its starts from rest); Final angular frequency (N2) = 540 rev-min-1 = 9 rev-s-1 and time taken (t) = 6s.
We know that angular acceleration (α) = [(ω2 – ω1) / t] = [(2 π N2 – 2 π N1) / t] = [2π (N2 – N1)/ 6]
= (2 π ( 9 – 0) / 6 = 3 π rad-s-2.Incorrect
Given that initially angular frequency (N1) = 0 (because its starts from rest); Final angular frequency (N2) = 540 rev-min-1 = 9 rev-s-1 and time taken (t) = 6s.
We know that angular acceleration (α) = [(ω2 – ω1) / t] = [(2 π N2 – 2 π N1) / t] = [2π (N2 – N1)/ 6]
= (2 π ( 9 – 0) / 6 = 3 π rad-s-2.Unattempted
Given that initially angular frequency (N1) = 0 (because its starts from rest); Final angular frequency (N2) = 540 rev-min-1 = 9 rev-s-1 and time taken (t) = 6s.
We know that angular acceleration (α) = [(ω2 – ω1) / t] = [(2 π N2 – 2 π N1) / t] = [2π (N2 – N1)/ 6]
= (2 π ( 9 – 0) / 6 = 3 π rad-s-2. -
Question 9 of 10
9. Question
1 pointsA wheel is rotated at 900 rev-min-1 about its axis. When power is cut off, it comes to rest in 1 min. The angular retardation is
Correct
Given that initial angular frequency (N1) = 900 rev-min-1 = 15 rev-s-1; Final angular frequency (N2) = 0 (because it comes to rest) and time taken (t) = 1 min = 60s.
We know that angular acceleration (α) = [(ω1 – ω2) / t] = [(2 π N1 – 2 π N2) / t] = [2π (N1 – N2)/ 60]
= (2 π (15 – 0) / 60 = 30 π / 60 = π / 2 rad-s-2.Incorrect
Given that initial angular frequency (N1) = 900 rev-min-1 = 15 rev-s-1; Final angular frequency (N2) = 0 (because it comes to rest) and time taken (t) = 1 min = 60s.
We know that angular acceleration (α) = [(ω1 – ω2) / t] = [(2 π N1 – 2 π N2) / t] = [2π (N1 – N2)/ 60]
= (2 π (15 – 0) / 60 = 30 π / 60 = π / 2 rad-s-2.Unattempted
Given that initial angular frequency (N1) = 900 rev-min-1 = 15 rev-s-1; Final angular frequency (N2) = 0 (because it comes to rest) and time taken (t) = 1 min = 60s.
We know that angular acceleration (α) = [(ω1 – ω2) / t] = [(2 π N1 – 2 π N2) / t] = [2π (N1 – N2)/ 60]
= (2 π (15 – 0) / 60 = 30 π / 60 = π / 2 rad-s-2. -
Question 10 of 10
10. Question
1 pointsA body of mass m is fixed to one end of a spring of force constant k and length l. The other end of the spring is fixed to a rod and the system is rotated with an angular velocity of ω, in a gravity free space as shown in the figure. The increase in length of the spring will be

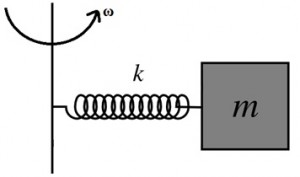
Figure Correct
Given that Mass of the body = m; Spring constant = k; length of the spring = l and the angular velocity of the system = ω.
We know that when the system is rotated, it will cause some centrifugal force, which will increase the length of the spring.
We also know that centrifugal force (F) = mω2 (l + x). [where x = Extension in the spring]
Therefore increase in the length of spring (x) = Centrifugal force / Spring constant = F / k
or, F = kx.
Equating two values of F, we get kx = mω2 (l + x) = mω2l + m2x
or, mω2l = kx – mω2x = x (k – mω2)
or, x = (mω2l / k) – mω2.Incorrect
Given that Mass of the body = m; Spring constant = k; length of the spring = l and the angular velocity of the system = ω.
We know that when the system is rotated, it will cause some centrifugal force, which will increase the length of the spring.
We also know that centrifugal force (F) = mω2 (l + x). [where x = Extension in the spring]
Therefore increase in the length of spring (x) = Centrifugal force / Spring constant = F / k
or, F = kx.
Equating two values of F, we get kx = mω2 (l + x) = mω2l + m2x
or, mω2l = kx – mω2x = x (k – mω2)
or, x = (mω2l / k) – mω2.Unattempted
Given that Mass of the body = m; Spring constant = k; length of the spring = l and the angular velocity of the system = ω.
We know that when the system is rotated, it will cause some centrifugal force, which will increase the length of the spring.
We also know that centrifugal force (F) = mω2 (l + x). [where x = Extension in the spring]
Therefore increase in the length of spring (x) = Centrifugal force / Spring constant = F / k
or, F = kx.
Equating two values of F, we get kx = mω2 (l + x) = mω2l + m2x
or, mω2l = kx – mω2x = x (k – mω2)
or, x = (mω2l / k) – mω2.


